Measuring distances to the stars: Parallax

In my post on Galaxies I noted the distance to the two galaxies concerned.
This raises the issue of measuring astronomical distances. The first step is
measuring distances to near by stars. This post considers how these
measurements are done.

It is possible to directly measure distances to stars that are relatively close to us by using trigonometry which is probably familiar from secondary school maths - eg COS, SIN, TAN, PI, radians and the like.
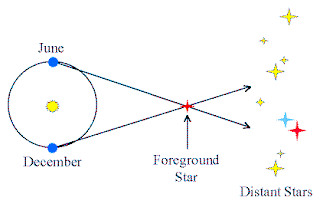
Nearby stars appear to move with respect to more distant background stars due to the motion of the Earth around the Sun. This apparent motion (it is not "true" motion) is called Stellar Parallax. (Stellar means star).
In the diagram at right , the line of sight to the star in December is different than that in June, when the Earth is on the other side of its orbit. As seen from the Earth, the nearby star appears to sweep through the angle shown. Half of this angle, is the parallax, p.

As even the closest stars are very far away the measured parallaxes are very small. Even the largest is less than an arcsecond.

If you are wondering what an arcsecond is, here is an explanation. A degree is 1/360 of a circle. An arcminute is 1/60 of a degree. An arcsecond is 1/60 of an arcminute. If you do the maths an arcsecond is 1/1296000 of a circle. For those with some maths background that is (π/648000) radians, which is approximately 1/206265 radian.

The closest star to the solar system, Proxima Centauri, has a parallax of 0.772-arcsec, which is the largest ever measured. (The closer a star is the larger its parallax). Incidentally the first parallax was measured in 1837 by Friedrich Bessel for the star 61 Cygni. We use photography and digital imaging techniques to measure parallaxes today. Increasingly, we measure parallaxes from space to avoid blurring due to the Earth's atmosphere.

The parallax relationship to distance can be expressed in a simple formula:
d = 1/p , where p is the parallax measured in arcseconds and d is the distance measured in parscecs. So what is a parsec.

"A star with a parallax of 1 arcsecond has a distance of 1 Parsec."

1 parsec (pc) is equivalent to:

* 206,265 AU (and AU is the distance between the Earth and the Sun about 149,598,000 Kms)

* 3.26 Light Years

* 3.086x10¹³ km

It can be argued that the parsec measure of distance is probably more "natural" than the light year as the latter is dependent on the length of one year (revolution of the Earth around the Sun) where as a parsec relates to a fraction of a circle. On the other hand the fraction of a circle used to define a parsec is pretty unusual, and relates to the realatively arbitrary decision to define degrees as 1/360 of a circle, and arcminute as 1/60 of a degree and arcsecond as 1/60 of an arcminute. Parsec as a "natural" measure is not in the same class as radian measure.

Here is an example of the calculation of parallax distances:

Alpha Centauri has a parallax of p=0.742-arcsec.

d = 1/p = 1/0.742 = 1.35 parsecs (pc)

There are serious limitations to this method:
If the stars are too far away, the parallax can be too small to measure accurately. In general, the greater the distance, the smaller the parallax, and so the less precise the distance measurement will be. The smallest parallax measurable from the ground is about 0.01-arcsec. This means that from the ground, the method of Trigonometric Parallaxes has the following limitations:
* good out to 100 pc
* only get 10% distances out to a few parsecs.
* only a few hundred stars are this close

The blurring of stars caused by the atmosphere makes it difficult to measure parallaxes to high precisions. Consequently the Hipparcos satellite was launched by the European Space Agency in 1989 with the aim of more precisely measuring stellar parallaxes. It can measure parallaxes to an accuracy of about 0.001-arcsec.
*Hiparcos has measured parallaxes for about 100,000 stars
*It can get a 10% accuracy for distances out to about 100 pc
*It can measure good distances for bright stars out to 1000 pc

Hiparcos represented a great leap in our knowledge of the distances (and motions) of nearby stars. For more information on Hiparcos visit the web site.